simple greenhouse gas models
Rotatable with your mouse after you click on “Read the rest of this entry“.
Most of randform readers might have heard that the socalled greenhouse effect is one of the main causes of global warming.
The effect is not easy to understand. There are two posts which give a nice intro to the greenhouse effect on Azimuth. One is by Tim van Beek and one is by John Baez.
The greenhouse effect can also be understood in a slightly more quantitative way by looking at an idealized greenhouse model.
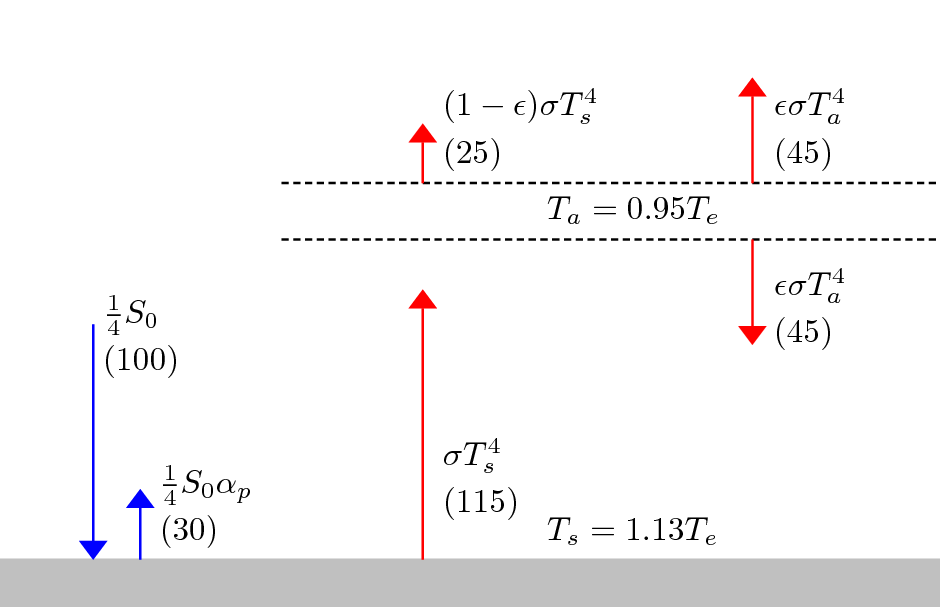
In the above diagram I now enhanced this idealized greenhouse model (as of Jan 2017) in order to get an idea about the hypothetical size of the effect of an absorption of non-infrared sunlight and it’s reradiation as infrared light, i.e. the possibly effect size of a certain type of fluorescence.
I sort of felt forced to do this, because at the time of writing (February 2017) the current climate models did not take the absorption of UV and near infrared light in methane (here a possible candidate for that above mentioned hypothetical greenhouse gas) into account and I wanted to get an insight into how important such an omission might be. The simple model here is far from any realistic scenario – in particular no specific absorption lines but just the feature of absorption and reradiation is looked at.
—————————————————————————–
insert April 24, 2023
My first email asking about the inclusion of shortwave (UV and near infrared) radiation into the radiative forcing of methane to Gunnar Myrhe was on Sept. 10, 2015. The last answer I got was in January 2017, when I pointed out in a new email that there are problems with the evaluation of solar radiation, as explained in the randform post Information about solar irradiance measurements sought (see also What is going on at the Sun?). The answer was basically that he is busy with meetings etc.
Meanwhile I had found out, by searching the internet, that the problems had been somewhat adressed.
That is in: Radiative forcing of carbon dioxide, methane, and nitrous oxide: A significant revision of the methane radiative forcing by M. Etminan1 , G. Myhre2 , E. J. Highwood 1 , and K. P. Shine it was found that
Methane’s RF is particularly impacted because of the inclusion of the shortwave forcing; the 1750–2011 RF is about 25% higher (increasing from
0.48Wm−2 to 0.61Wm−2) compared to the value in the Intergovernmental Panel on Climate Change (IPCC) 2013 assessment; the 100year global warming potential is 14% higher than the IPCC value.
The new value came from the inclusion of absorption spectra with shorter wavelengths.
The new value was inserted into climate simulations in:
Understanding Rapid Adjustments to Diverse Forcing Agents
Accordingly the new IPCC report writes in chapter 7: 7.3.2.2 Methane:
The SARF for methane (CH4) has been substantially increased due to updates to spectroscopic data and inclusion of shortwave absorption (Etminan et al., 2016). Adjustments have been calculated in nine climate models by Smith et al. (2018b). Since CH4 is found to absorb in the shortwave near infrared, only adjustments from those models including this absorption are taken into account. For these models the adjustments act to reduce the ERF because the shortwave absorption leads to tropospheric heating and reductions in upper tropospheric cloud amounts. The adjustment is –14% ± 15%, which counteracts much of the increase in SARF identified by Etminan et al. (2016). Modak et al. (2018) also found negative forcing adjustments from a methane perturbation including shortwave absorption in the NCAR CAM5 model, in agreement with the above assessment. The uncertainty in the shortwave component leads to a higher radiative modelling uncertainty (14%) than for CO2 (Etminan et al., 2016). When combined with the uncertainty in the adjustment, this gives an overall uncertainty of ±20%. There is high confidence in the spectroscopic revision but only medium confidence in the adjustment modification.
A very new evaluation in Methane’s Solar Radiative Forcing finds:
Including the impact of SW absorption on stratospheric temperature increases tropopause SARF by 0.039 W m−2 (or 7%) compared to the LW-only SARF.
The article Understanding Rapid Adjustments to Diverse Forcing Agents however also evaluated what a 2% increase of the solar constant parameter shows in the climate models and found (see Fig. 1) that the radiative forcing increases as if one would double the CO2 parameter or triple the CH4 parameter.
—————————————————————————–
The above diagramm shows the earth temperature in Kelvin as a function of two parameters, as given by this enhanced model. The two parameters can be seen as being (somewhat) proportional to densities of a hypothetical greenhouse gas, which would display this type of fluorescence. That is the parameter x is seen as (somewhat) proportional to the density of that hypothetical greenhouse gas within the atmossphere, while y is (somewhat) proportional to the density near the surface of the earth. Why I wrote “somewhat” in brackets is explained below.
The middle of the “plate” is at x=0, y=0 (please hover over the diagram) which is the “realistic” case of the idealized greenhouse model, i.e. the case where infrared absoptivity is 0.78 and the reflectivity of the earth is 0.3. The main point of this visualization is that linearily increasing x and y in the same way leads to an increase of the temperature. Or in other words, although raising x by a certain amount leads to cooling this effect is easily trumped by raising y by the same amount.
As far as I learned from discussions with climate scientists the omission of non-infrared radiation in the climate models was mostly motivated by the fact that an abpsorption of non-infrared is mostly happening in the upper atmossphere (because methane is quickly rising (but there are also circulations)) and thus leading rather to a global cooling effect than a global warming effect and so it in particular doesn’t contribute to global warming. The enhanced simple model here thus confirms that if absorption is taking place in the upper athmossphere then this leads to cooling. The enhanced model however also displays that the contribution of methane that has not risen, i.e. methane that is close to the earth surface, is to warm upon absorption of non-infrared light and that the effect of warming is much stronger than the cooling effect in the upper athmosphere. Unfortunately I can’t say how much stronger for a given amount of methane, since for assessing this one would need to know more about the actual densities (see also discussion below and the comment about circulations). Nonetheless this is a quite disquieting observation.
I had actually exchanged a couple of emails with Gunnar Myrhe, the lead author of this corresponding chapter in the IPCC report, who confirmed that non-infrared light absorption in methane hasn’t sofar been taken into account, but that some people intended to work on the near-infrared absorption. He didn’t know about the UV absorption that I had found e.g. here (unfortunately my email to Keller-Rudek and Moortgat from 2015 whether there is more data for methane especially in the range 170nm-750nm stayed unanswered) and thanked for pointing it out to him. He appeared to be very busy and as drowning in (a lot of administrative) work, so that I fear that those absorption lines still might not have been looked at. That is also why I decided to publish this now. I sent a copy of this post to Gunnar Myrhe, Zong-Liang Yang and John Baez in June 2017, where I pointed out that:
I have strong concerns that the estimations of the global warming potential of methane need to be better assessed and that the new value might eventually be very different then the current one.
– but I got no answer.
The Wikipedia entry on the Idealized greenhouse model is based on course notes of the course 387H: Physical Climatology by instructor: Zong-Liang Yang where he used this simple model for motivating more complicated models with many layers:
Solution of idealized greenhouse model with emissivity by author Incredio, licence CC BY-SA 3.0
As said, I now enhanced this simple model in a certain way in order to get some insight into the temperature sensitivity of absorption of non-infrared light and it’s conversion into infrared light. I currently don’t have access to a commercial computer algebra system and I sofar haven’t got along with the Sage syntax, so in particular solving spherical Navier-Stokes equations as done in GCM’s is quite out of reach. So I tried to use this enhanced model with Julia. The code is below.
The enhanced model is depicted in the following image:
The notation is as in the Wikipedia article (see first image above), with a few alterations. That is $latex S=\frac{1}{4}S_0 = 341 W/m^2$ is here one fourth of the total incoming solar radiation (the factor one fourth is because the area of a sphere (i.e. here the earth) is four times the area of its circular shadow, this is e.g. motivated here) and $latex \alpha_p$ is set here $latex \alpha_p = \rho_s$ where I chose $latex \rho$ as in “reflected”. I kept the notation for the subscripts as they were already used for the temperatures $latex T$ in Wikipedia, so the subscripts are $latex s$ as in “surface” and $latex a$ as in “atmosphere”. The symbol $latex \epsilon_{IR}$ denotes the absorptivity/emissitivity of infrared light in the atmossphere (in the Wikipedia entry just $latex \epsilon$), likewise $latex \epsilon_{UV}$ denotes the absorptivity/emissitivity of ultraviolet and other noninfrared light, which is here now assumed to be reradiated as infrared light within the atmossphere.
As there seems no “simplify” in Julia, I had to shuffle the algebraic expressions by hand, which is of course error-prone, but I hope there are no mistakes. Below the code and intermediate steps.
Anyways if you look at the code then you see that $latex \epsilon_{UV}$ and $latex \rho_s$ are dependent on the variables delta1 and delta2. In the model they describe “small deviations” from some standard values. delta1 describes the deviation from the UV absorptivity and delta2 the deviation from the reflectivity of the earth. The idea behind is that if there is some greenhouse gas which absorbs noninfrared and reradiates this as infrared then as delta1 increases the noninfrared absorptivity of the atmosshpere, this is as if there would be “more of that absorbing” greenhouse in the atmossphere. So in the beginning I wrote the word “somewhat” in brackets, because I don’t know the exact relations between absorptivity and density of a greenhouse gas, apart from this I don’t know much about actual densities (see comment about circulation and this post). Likewise delta2 could describe a “more of that greenhouse gas” at the surface of the earth. In the diagram delta1 is x and delta2 is y.
#code is GPL by Nadja Kutz
S= 341.5
deltaAt = 0.0
deltaSur = 0.0
epsuv = 0.0+deltaAt
epsir = 0.78
#epsir=0.78 is corresponding to usual CO2forcing
rhos = 0.3-deltaSur
sigma = 0.00000005670367
Ts= (1/((1-0.5*epsir)*sigma)*(((1-rhos)*(1-epsuv) -0.5*(-epsuv*(1-rhos)-rhos + (1-epsuv)^2*rhos))*S))^0.25
Ta=(1/((epsuv + epsuv*(1-epsuv)*rhos + epsir)*sigma)*((1-(1-epsuv)^2*rhos)*S-(1-epsir)*sigma*Ts^4))^0.25
println(“deltaAt=”,deltaAt,” deltaSur=”,deltaSur,” Ts=”,Ts,” Ta=”,Ta)
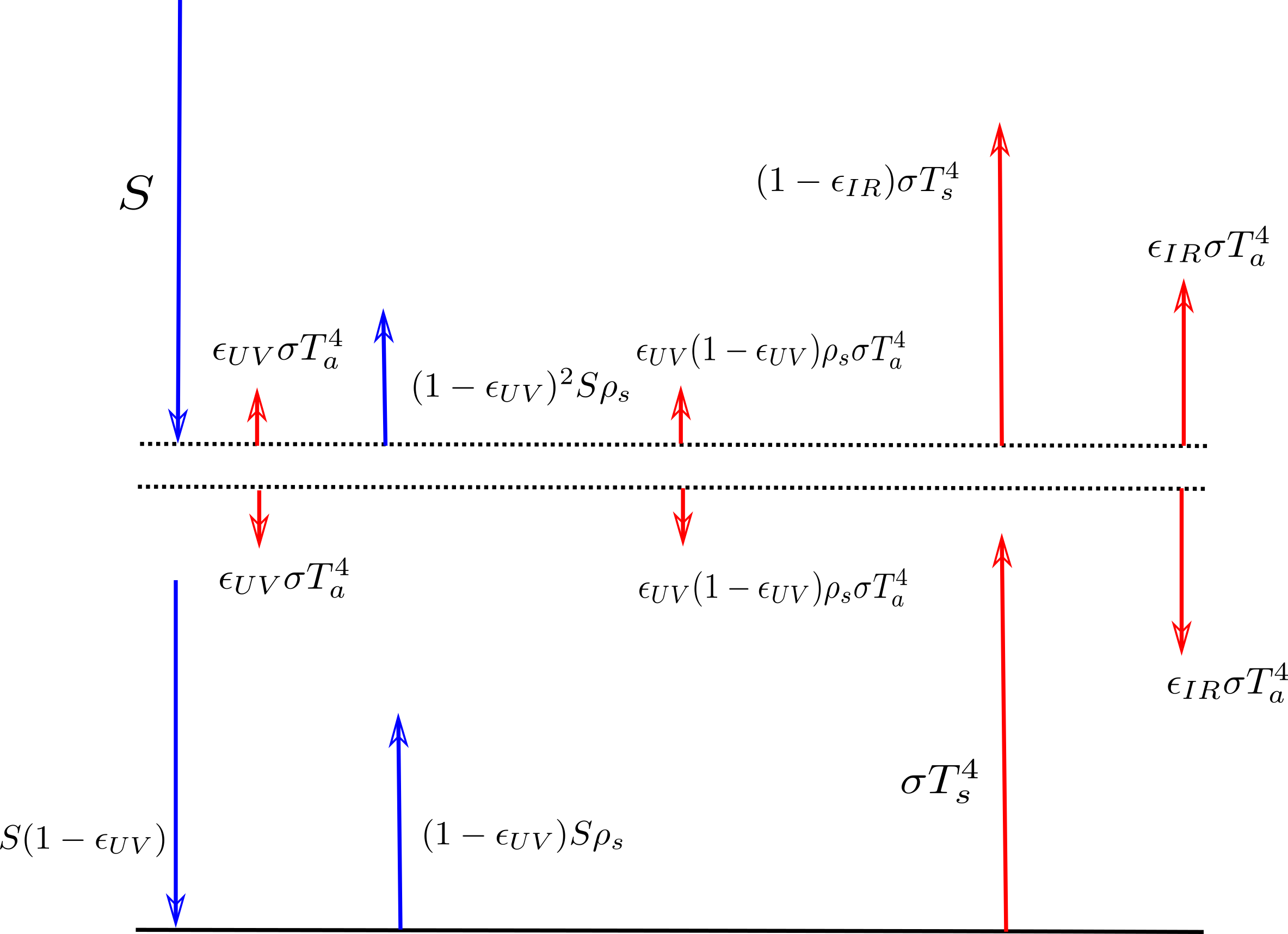
#calculation see image Greenhouse.svg
#Term 1
-(1-(1-epsuv)^2*rhos)*S + (epsuv + epsuv*(1-epsuv)*rhos + epsir)*sigma*Ta^4 + (1-epsir)*sigma*Ts^4
#Term 2
(1-rhos)(1-epsuv)*S + (epsuv + epsuv*(1-epsuv)*rhos + epsir)*sigma*Ta^4 – sigma*Ts^4
#Term1 + Term2 !=0
-epsuv (1-rhos)*S -rhos*S + (1-epsuv)^2*rhos*S + 2* (epsuv + epsuv*(1-epsuv)*rhos + epsir)*sigma*Ta^4 + (-epsir)*sigma*Ts^4
#Solve Term1 + Term2 !=0 for Ta
Ta^4= -1/(2*(epsuv + epsuv*(1-epsuv)*rhos + epsir)*sigma)*((-epsuv*(1-rhos)-rhos + (1-epsuv)^2*rhos)*S + (-epsir)*sigma*Ts^4)
#Into Term 2
(1-rhos)(1-epsuv)*S -0.5*((-epsuv*(1-rhos)-rhos + (1-epsuv)^2*rhos)*S + (-epsir)*sigma*Ts^4)- sigma*Ts^4
#Simplify
((1-rhos)(1-epsuv) -0.5*(-epsuv*(1-rhos)-rhos + (1-epsuv)^2*rhos))*S + (0.5*epsir-1)*sigma*Ts^4
#Solve for Ts
Ts= (1/((1-0.5*epsir)*sigma)*(((1-rhos)*(1-epsuv) -0.5*(-epsuv*(1-rhos)-rhos + (1-epsuv)^2*rhos))*S))^0.25
The plot of the function (with some help from Tim) can be got from this code:
function Surfacetemp(deltaAt,deltaSur)
S= 341.5
epsuv = 0.0+deltaAt
epsir = 0.78
#epsir=0.78 wird als CO2forcing angenommen
rhos = 0.3-deltaSur
sigma = 0.00000005670367
(1/((1-0.5*epsir)*sigma)*(((1-rhos)*(1-epsuv) -0.5*(-epsuv*(1-rhos)-rhos + (1-epsuv)^2*rhos))*S))^0.25
#Ta=(1/((epsuv + epsuv*(1-epsuv)*rhos + epsir)*sigma)*((1-(1-epsuv)^2*rhos)*S-(1-epsir)*sigma*Ts^4))^0.25
end
using Plots
plotly()
x = y = linspace(-0.1, 0.1, 20)
plot(x,y,Surfacetemp,st=:surface)
thanks to Tim for helping me deciphering the Julia documentation
August 3rd, 2018 at 7:21 am
Why isn’t this published on John Baez blog?
By the way he is currently bashing climate denialists on Twitter:
https://mobile.twitter.com/johncarlosbaez/status/1025044543513612288/photo/1
…so maybe he is not so happy with what you wrote here.
August 3rd, 2018 at 8:24 am
I don’t know, I haven’t heard from him in a while. He seems to be very busy teaching category theory.
Yes I saw that and I was already wondering, that he so clearly dismissed Scott Wagners arguments, because I found at least one of them per se not so easily dismissable. And I also didn’t find John Olivers arguments convincing. If Scott Wagner takes money from the oil industry then this makes him less credible, but that doesn’t mean either that all of his arguments need to be wrong. In particular he might be right by accident for some issues.
That is the earth orbits in a nearly circular orbit around the sun, so there is not much “moving in and out”. But even if there is, I think it is rather clear that Scott Wagner was probably not forgetting about the ellipticity of the earths orbit but that he meant the average distance between earth and sun.The seasons are due to the changing angle of the earths axis with respect to the orbit plane.
The earth might at some point crash into the sun, because it is loosing energy but then the sun is probably loosing quite a bit of mass. I have quickly looked for concrete measurements of the earths distance to the sun but I haven’t sofar found anything. I imagine that if there would be big alterations we would have heard of that, but who knows….after looking a bit at the state of science and media I wouldn’t wonder too much if not. So I find this argument actually not so easily dismissable and per se a rather important point that apriori needs to be checked.
What about the heating by humans? The earth has according to Wikipedia a surface of $latex 510*10^{15} m^2$, multiplied by the above average power $latex 341 kW/m^2$ this is about $latex 174*10^{18} W$. If a human would convert all eaten energy into heat than as I had calculated here this would be for 1500kcal about 1.743 KWh per day, i.e. $latex 1743 Wh/24h=72.625W $ There are currently $latex 7.6*10^9$ people on earth so this is $latex 72.625W*7.6*10^9=551*10^9W $ so roughly about a factor of $latex 10^9$, i.e. one billion off from from the sun’s average power on earth. So this appears indeed rather small, apart from the fact that that one has to compare this with the “heat” that would be produced via the decay of food.
So I dont have no time to do bigger calculations but I think the earths orbit is something that has to be looked at in principle, the heat produced by humans is something I would leave out in calculations for the moment.
If mankind would need to alter the earths orbit then this will need a lot of science and I am not sure if “society” is doing its best here.
August 5th, 2018 at 8:20 am
John Baez seems to implicitly comment on your remark with the correction that the assumption of 1500 kcal per person is way too small – he is right – a human needs about 2500 kcal per day and thus 115 Watts and not 72 as you calculated. He furthermore discusses that people use about 475 Watts of electricity, so this is about 4 times the amount of power you considered negligable in contrast to the sun, but then climate scientists freak out about electricity consumption and not about human food. You contradict yourself.
August 5th, 2018 at 9:58 am
I doubt that he commented on what I wrote, since he told me that he reads this blog not very often.
The 1500 kcal is what is probably to be expected as a future food average. I thought that human heat doesn’t play a big role because it is mostly reradiated, it basically enters the above balance. It is the accululation of gases in the athmossphere that changes the temperature. Thus what may play a role is actually rather the CO_2 contributions of humans.
Let’s do a quick estimation:
Sorry I have only found in the german Wikipedia Gasaustausch an info about the conversion of O_2 into CO_2:
which says that of 1 liter air approx. 170 ml of O_2 is inhaled and 130ml exhaled. So about 17% of inhaled air is O_2 and 13% is re-exhaled. That is a bit off of what the english Wikipedia says about the average air:
, but this might be due to the different air pressures at different heights. So 70mL=0.07L of the 170 mL inhaled oxygen is converted and I assume it is probably mostly converted into CO_2 that is 70/170= 41%. The air volume per minute is in the english wikipedia 6 L/min, in the german it is 7.6 L/min, so lets take 7 l per minute, so in a lifetime of 70 years this is 0.07L*7*60*24*365*70=18028080L according to google calculator, so about 18 million Liter O_2 is converted into CO_2 per person and lifetime. So the current 7.6 billion people will convert 18*7.6*10^15 L= 14*10^16L.
Unfortunately I couldnt find any numbers about the oxygen volume on earth, so lets assume the relevant atmossphere is 15 kms thick. The earth radius is 6371 kms that gives a volume of (6371)^3*3.14*4/3 kms^3 adding 11 km to the radius and deducing the earth volume and taking 20 % oxygen thus gives:
((6382)^3-(6371)^3)*3.14*4/3*0.2 km^3= 1123510552.79 km^3 =
1.12* 10^9 km^3=1.12*10^9*10^27m^3=1.12*10^9*10^27*10^3L= 1.12*10^(9+27+3)L=1.12*10^39L So roughly if there would be no 02 production (like by plants) there would be an oxygen volume for way less (I dont know the lethal proportion) than 10^39/10^16 =10^23 generations of humans. So at the moment this doesn’t look dramatic.
But what about the CO2?
Taking a factor of 0.000407 for the fraction of CO_2 gives 2286343.97 L= 2.3*10^6 L So human breath conversion of 14*10^16L might contribute significantly to CO_2 percentages.
Please take the calculations in this comment here with utmost caution, as I didn’t check them and it is very likely that I missed a factor here and there. This calculation is just for roughly estimating whether it might be relevant to look into this further and I currently think yes.
August 6th, 2018 at 9:22 am
What is accululation?
This is ridiculous. You shuffle around some numbers and brackets and cryptic ^ and chemical abbreviations and you think you can display some magic which tells us that human breath might be dangerous or what?
August 6th, 2018 at 10:11 am
@cindy
accululation is a missprint -it should read accumulation. I was in a bit of a hurry, when I wrote the comment above. That is socalled greenhouse gases are stored and again stored (I.e. accumulated) in the air and sofar nobody removed those gases and those gases seem to be one reason why solar light is leading to more heat up on earth.
I didn’t say that human breath is dangerous, I just said that by the above calculations that human breath implicitly might contribute to rather fastly rising temperatures on earth due to the accumulation of the CO_2 in breath in air. One in particular has to compare this to the decay of plants, which also produce CO_2 if they are not eaten by humans or animals.
You can see this “number shuffling” as a magic if you want, it is though a “magic” that has been developped by very careful observation of natural laws and a lot of humans trying to make sense of that. It has sofar taken people to the moon, so it hasn’t been too unsuccessful in the past, in fact science had sofar been much more successful than any other attempt in doing “magic”, i.e. in making people “do” things that were quite unthinkable once. But of course this is no guarantee for the future. Physical laws can change any second and then a lot of physicists and mathematicians are pretty useless. I keep saying this on this blog.
The ^ means “raised to the power of”, so 10^2 is 10*10=100 and 10^3=10*10*10=1000. The equality sign means that all those expressions are considered to be the same “thing”. The brackets are an abreviation, which makes use of the distributive law between multiplication and addition and for writing sums in exponentials. The abbreviations for chemicals are explained in Wikipedia. CO_2 is carbon dioxide.
August 7th, 2018 at 9:10 am
It is not only plant decay that makes plant produce CO2 but you in particular forgot to mention soil respiration.
August 8th, 2018 at 8:55 am
nad wrote:
So why do you then write posts about oxygen recesseion?
August 8th, 2018 at 9:51 am
@Dumuzid
Thanks for pointing out the soil repiration link.
I wrote this mainly because there is still a big air volume, but then things get thighter.
OK let’s look for example at Hypercapnia.
The german Wikipedia writes:
From a concentration of 1.5% the respiratory minute volume increases by more than 40%, no citation at that concentration the english Wikipedia writes there (and cites Lambertsen, Christian J. ( “Carbon Dioxide Tolerance and Toxicity”. ) is to be expected a “mild respiratory stimulation ” after an exposure for longer than a month. An immediate carbon dioxide poisoning seems to take place in both Wikipedias at around 8%. The effects of higher dosis and long term exposure seem to be more difficult to establish, in particular it seems that Hypercapnia doesn’t follow the usual Haber’s rule. Google calculator says that: 0.08/0.0004=200. So if one takes the above CO2 estimate than about 200* 2.3*10^6 L = 4.6*10^8L of CO2 in the air will make air rather poisonous. So if the above estimation of 14*10^16L is right than humans will exhale about 3*10*8=300.000.000 times more CO2 than that poisonous dose….but of course there are still plants producing oxygen….
August 10th, 2018 at 7:18 am
There is the article Global land change from 1982 to 2016 which says that
So this suggest that plants produce more oxygen!
This by the way has also been reported in a german mass media outle (since you were suspecting the media might not report):
http://www.spiegel.de/wissenschaft/natur/mehr-baeume-auf-der-nordhalbkugel-die-erde-wird-gruener-a-1222240.html
Are you sure that your estimations are at all useful? You write:
But if you say this is shaky then maybe it is even too shaky to conclude that one should “look further into this”.
August 10th, 2018 at 8:57 am
@Dumuzid
Thanks for pointing out the article.
Another effect of those calculations is to see how long it takes to do them.
And it is not only the calculaitons themselves but also the assumptions that have been made here that are shaky, like in particular the absolute air volume.
But anyways as we know the biggest CO2 production is via fossil fuel usage, so let’s compare human breath to global fossil fuel CO2 production.
It is written in here that:
What is the volume of one ton CO2? Wikipedia says that at 0°C and a pressure of 1013 hPa CO2 has a density of 1.98 kg/m^3 so roughly this gives 1000kg/1.98kg m^3= 505.0 m^3.
This is in the same range as the 556.2 m^3 that has been found here for 25 °C. So assume 556m^3 is correct then this is 32.5*10^9*556*1000L= 1.8*10^16L We had for human breath 14*10^16L/70 CO2 volume in a year that is 0.2*10^16 L. So annual CO2 from fossil fuel emissions are about 9 times more than human breath exhalations or human breath is about 11% the size of global CO2 fossil fuel emissions or 0.2/(0.2+1.8) =0.1, i.e. 10% of fossil fuel and human breath emissions together.
June 15th, 2019 at 11:47 am
There is a big discussion in the german media due to the ultra right wing politician Alice Weidel: https://www.tagesschau.de/faktenfinder/weidel-klimawandel-101.html
A citation from the article with tranlsaiton:
Isn’t it possible to explain this green house effect with easy plain words to clarify things? Don’t you want to engage in the debate about this on Twitter?
June 15th, 2019 at 12:41 pm
@Bratfunne
The greenhouse effect describes what happens with earth when it is impacted with radiation. In order to make things easier imagine that radiation would only consist of visible light. If you have a mirror around you then light gets reflected and you don’t even see it. If you don’t have a mirror then your skin is reflecting but also absorbing something of that light. The absorbed light makes you heat up a bit and then you may reradiate something of that heat. Heat is infrared radiation. If the light is more or less constant this process will be more or less stay the same, i.e. you will stay at a certain temperature (forget about metabolism for simplicity). You can calculate that temperature more or less well, if you know how the material (here your skin and body) absorbs radiation. If you put on black clothes you absorb more light and you will stay at a higher temperature than with white clothes.
The CO2 is a bit like a garment. That is one knows how CO2 absorbs radiation and so one can estimate what a change in CO2 does to the earth temperature. But those calculations are hard and complicated, as you can imagine. As said the above is just a very simplified version. So yes one can discuss how big the role of CO2 is in here, just like you can discuss how much you heat up if you put on a black or just an antracite cloth. But one thing should be clear: If the sun radiates more light then more CO2 makes things even worse. So CO2 acts a bit as a kind of trigger.
No I don’t want to engage in those Twitter discussions and in fact I am currently thinking about shutting down this blog.
June 15th, 2019 at 6:24 pm
Don’t you think this is a bit too arrowgant? Please carry on and tell us in simple words what this post is about.
June 17th, 2019 at 1:50 pm
Sorry, but I currently don’t have the time for lengthy explanations let alone calculations. As you can see at the other posts there are some not so easy local problems, which became more urgent. Unfortunately on top of that some bad health problems in my direct vicinity occurred.
OK. So here in more simple words what this post is about:
In the idealized model it is for simplicity assumed that the atmossphere absorbs only infrared light. With the garment picture above that means that your garment looks transparent but is able to absorb heat. So heat that comes from your “body” (here the earth) is absorbed and send back (“reflected”), i.e. the garment keeps you warm.
In the above post I do a very rough estimation in this idealized model of what happens if the atmosphere could absorb ultraviolet or visible light (=non-infrared light) and can turn that into heat.I.e. I assume the garment is not transparent.The calculations show that if your “garment” is far from the body this has a cooling effect (imagine the “garment” is an umbrella or tarp), however it would heat you up more than a transparent garment, if the “garment” would be close to the body.
As a matter of fact for some parts of the garment (“some greenhouse gases” in the atmosphere) it had been assumed (I asked at the IPCC about methane, see remark above) that the garment is “transparent” because the calculations are so complex that you have to simplify and the greenhouse gas methane moves up rather quickly anyways. The big question here is whether such an assumption may eventually lead to a too idealized overall picture of the situation, i.e. whether you do omit very crucial components and maybe things heat up way faster than assumed.
I didn’t finish the calculation, that is in the above I in particular do not care about “how thick the garment is” but just try to cast that effect of cooling vs. heating, depending on garment vicinity to the body, into simplified formulas. The formulas reveal that heating up goes much “faster” than cooling down.
As said neither did I finish the calculation, nor did I use in-depth mathematical methods, but I informed the IPCC. On top of that it seems that the sun seems to have started to radiate stronger in certain colours. In addition in the meantime the elevated sun radiation measurements by LISIRD had been “corrected down” and I think that “correction” is false because another dutch satellite showed a similar higher radiation. I made that public on John Baez’Azimuth blog (a blog which was previously discussing climate science findings), but got no answer. I asked at the World radiation center if they know about other measurements but got not answer. Frankly I am afraid about the possible results. It may be that global warming had been underestimated by quite a bit.
June 19th, 2019 at 7:22 am
We heard that before! Nobody wants to hear again and again those apokalyptic messages! What’s the use of them? Maybe that you want more attention?
June 21st, 2019 at 6:23 pm
Well it seems some humans prefer to know in advance how hot things can get and eventually how soon – even if there are high uncertainties and irrespective of the question whether adjustments are possible.
July 14th, 2019 at 6:55 am
I can’t see anything that’s rotable with my mouse.
Did you see Rhett Allain’s story: Should You Wear White or Black on Hot Days? Here’s the Data? He nicely shows how one can see heat with infrared cameras, So don’t worry -there are enough masurements who take care of all of this.
July 14th, 2019 at 9:36 am
Yes sorry it seems the visualization doesn’t work anymore due to some software upgrade. I currently don’t have the time to look into that (for example right now we are actually busy fixing our kitchen sink). In particular as already said in a comment I am thinking about shutting down this blog.
Thanks for the article link – experimental physics with T-shirts sounds like fun :)
And yes there are measurements, but amongst others I am not sure how well a higher near-ground absorption -like due to methane as thematized in the above blog post would be noticable – especially on a world scale. Interesting in this context is the red blob over the Sea of Okotsk in this Video.
And as said already above – even if you notice- you have to make decisions about what to care.
July 15th, 2019 at 8:47 pm
Again?! Maybe selfmade fixes not so good…. :-)
Please share pictures :-)
July 16th, 2019 at 10:00 am
Nad you wrote in that other comment:
Don’t you have meanwhile a job so that you could afford a cleaning help and an plumber or as you germans say a Anlagenmechaniker für Sanitär-, Heizungs- und Klimatechnik ?
July 17th, 2019 at 9:02 am
Victor wrote:
No not again that is – knock on wood – my sewage pipe installation was still OK. This time it was the cold water freshwater pipe of the sink armature which was so corroded (after 12 years….!) that it first started dripping and then emanating small fountains …. and this of course on a sunday. See the stain on the wall next to the pipe:
Tim then tried to close the freshwater tap (on the right on the angle valve, above the tap with the blue dot there is a tap which had the same knob as for the warm water on the left):
…but the knob (plastic) couldn’t cope with the jammed tap, i.e. it started overruning without gripping. Since it was sunday we didn’t really wanted to mess around with the freshwater system (which has a 3 bar pressure) and thus decided to hire a plumber. You have to be a bit careful in Berlin – there are quite some internet websites which offer 24 plumbing, these are however eventually sort-off-rip-off sites. That is you call there and they promise a plumber, who will then eventually however arrive only on monday, while the website is of course still asking for a commission. Anyways we were still lucky to find a plumber who was there within an hour, but well this is expensive. What did he do? He knew that it is harmless to just tear off the plastic knob with violence and then close the tap with a gripper. He didn’t install though a new angle valve, because this was not included in the emergency service. The costs were: 40 Euro for every started plumbing hour, double cost because of sunday, 25 Euros for driving, plus 19 % tax makes 125 Euros (around 140 US$) for closing a tap.
Our house-plumber (who has no 24 service) called me later the week and suggested that it is probably save to open the fresh water tap again with a gripper and to install a new angle valve sometime later, because he is fully booked out.. So Tim and me bought a new armature. Tim installed it (dismantling the old armature was actually physically demanding) and with a deep breath we opened again the tap, which -as our house-plumber- promised still worked.
I have to work considerably longer than an hour for 125 Euros, that Bibi might answer your question, at least in part.
July 21st, 2019 at 10:06 pm
As a supplement to my remark about the sea of Okhotsk (and the link to fuel production there) you may eventually want to read about efforts to reduce methane emissions in fuel production by the Oil and Gas Methane Partnership (OGMP): Third-Year Report. For example (page 9):
The 9 core emission sources of methane are:
As a matter of fact (p.8):
September 16th, 2019 at 6:35 pm
Have you meanwhile checked about the distance? Isn’t it that a closer distance would lead to more global warming and thus the effect of “global warming” would not be anthropogenic ?
September 16th, 2019 at 8:46 pm
No. I haven’t.
Even if we would spiral into the sun then if you believe in the greenhouse gas effect there would still be an anthropogenic component. But yes of course if we would be rapidly spriraling into the sun then this component would not make a tremendous difference anymore.
September 17th, 2019 at 8:06 am
WTF!! you want suggest that we spiral into the sun?!
September 17th, 2019 at 9:42 am
No. I don’t want to suggest that we (rapidly) spiral into the sun, I wrote:
Maybe I will look into this one day, but alone keeping track of using the right definitions takes time. It’s a complicated subject. So if you want a fast answer then this blog here is currently not the right place to get one.
October 7th, 2019 at 7:55 am
@Mandy
A quick glance at NASA webpages shows earth is moving away from sun:
http://curious.astro.cornell.edu/observational-astronomy/41-our-solar-system/the-earth/orbit/83-is-the-distance-from-the-earth-to-the-sun-changing-advanced
And nad didn’t mention that there is in addition tidal effect on sun which makes earth go away.
October 7th, 2019 at 8:18 am
if you look for definitions then instead looking at time definitions, better start with definition distance earth-sun:
October 8th, 2019 at 7:20 pm
You had been linking to and citing from the Astronomy Department of Cornell University. On that page two possible causes for a changing eath orbit are mentioned, namely the tidal interaction between sun and earth (“this is a very tiny effect.”), which -yes- I didn’t mention in my comment and the one due to nuclear fusion, which I casually mentioned with “but then the sun is probably loosing quite a bit of mass.”
I am not an astronomer and so the fact that the earth is loosing energy (see my remark: The earth might at some point crash into the sun, because it is loosing energy but then…) may have such a tiny effect on the earth orbit that it is eventually not noteworthy on solar system time scales. I don’t know.
The Cornell webpage mentions the tidal interaction between moon and earth which leads to a slower rotation of the earth. I could also imagine that the earth acting as a geodynamo uses up rotational energy (while in this context one should also think about effects of the heliocentric current sheet).
So I have quickly looked whether I can find anything about how a slowdown of the earth rotation interacts with the earth orbit but have found nothing. I found only an article from Dec. 1963 by Robert J. Nauman where “torque-producing forces acting on satellites” are investigated. He writes:
Strictly speaking this is about how a body on an orbit is dragged and not how a drag may influence an orbit but loosely speaking in that vain I imagined there could be some effect of a “drag” (different rotation speed) on the orbit of the earth-moon system around the sun.
I am sorry that this is all very hand-wavy but thats also why I wanted to see measurements.
I was looking for time definitions as I thought that a change in orbital speed with respect to the fixed stars would eventually be the easiest way to find out about orbital changes.
October 13th, 2019 at 10:21 am
Are you sure you know what you are talking about?
Tagesschau says it is wrong that human breath leads to increasing CO2 levels (which is by the way again a statement by right wing party AFD):
translation:
https://www.tagesschau.de/faktenfinder/kohlendioxid-atmung-brandner-101.html
October 14th, 2019 at 1:48 pm
@Bratfunne
Did you see my comment? I already asked whether she knows how shaky she is at
comment-60163″ and got no answer….but then we are meanwhile talking about the earth spiralling into the sun ;)
October 14th, 2019 at 7:54 pm
Didn’t you know – Earth will be propelled to Andromega, like space ship. 😂
October 29th, 2019 at 8:27 pm
While we are waiting for answer -on other thread: nad started explain how sun engine really looks like :
🤦
https://www.randform.org/blog/?p=6731#comment-60649
🌟
💫
November 28th, 2019 at 7:14 pm
@Victor @Dumuzid
I don’t quite get, why you are here at all waiting for an answer. These questions are scientifically settled.
Haven’t you noticed that the EU had issued a climate emergency declaration?
November 30th, 2019 at 8:14 am
@Violonce
We are not waiting for an answer. I was just joking around a little bit. I read this blog mostly for entertainment. Author used to be funny. Not so funny anymore so. Author is getting old.
December 14th, 2019 at 12:26 pm
@Bratfunne, Dumuzid, Victor and others.
I try to speak only about things which I perceive as sufficiently understood. It is clear that climatic processes are so complex and gigantic that it is not so easy to keep an overview.
Tagesschau doesn’t say that “it is wrong that human breath leads to increasing CO2 levels ” it says (actually Mr. Rohwedder says) that
“The amount of carbon dioxide in the atmossphere remains thus largely stable” (….in a process which includes breathing). And this is correct.
The crucial point here, I think, is how fast changes are happening and whether ecosystems can adapt and in particular whether relevant cycles break.
Let’s investigate this mechanism.
Photosynthesis has basically been the only huge oxygen (abbreviated as O2) producing process on earth, and it is to a great extend done by plants.
It is true that via photosynthesis one carbon atom of carbon dioxide (abbreviated as CO2) will be transformed into one carbon atom in sugar (“food”), which may then be eaten and eventually exhaled by humans and then eventually recaptured by plants. So very simplified: exhaled CO2 comes from plant captured CO2. Likewise Respiration of humans and animals basically reverses photosynthesis. So oxygen and CO2 amounts should stay roughly constant, if the respective amounts of plants and plant eaters stay roughly constant, like by appropriate regrowth. This is what is probably meant by “comes from its own metabolism” (see citation Tagesschau). It can be seen as a “cyclic process”. This cyclic process is amongst others “fueled” by sun light. Without sun light this process would break down. But of course there are also other “fuels” like e.g. water.
The cyclic process would also be disturbed if there are for not enough plants to produce enough O2 and I think this might happen before there will be not enough plants to eat, like in this example: randform link.
In particular there are also other natural processes which use oxygen and those uses of oxygen had been balanced to some extend by plants which were not eaten, i.e. had not been part of the above cycle but for example part of the nitrogen cycle. In this cycle some microorganisms capture O2 to produce Nitrate from ammonium (the ammonium comes e.g. from dead plants or from artificial processes like the Haber process). Nitrate can then again used by plants as a “food”. But there are also organisms see e.g. ( here) which produce another bad greenhouse gas namely laughing gas (nitrous oxide) in that context.
If there are e.g. less plants then at one point O2 production via plants might be less than “needed” and so oxygen amounts will decline. If oxygen amounts decline and CO2 amounts would stay constant then the percentage of CO2 in air rises as a percentage with respect to O2. Likewise if amounts of certain soil bacteria rise then this might also reduce O2 percentages. As mentioned above something like this happened in an experiment (see again randform link).
The above mentioned cycles are rather stable that is little disturbances can usually be balanced. So for example: a higher CO2 concentration in air leads usually automatically to more plant growth and thus to more O2 production (for higher temperatures this works though apparently not so good anymore) and so too high CO2 percentages may rebalance to some extend. But this rebalancing doesn’t work forever. There are also processes like CO2 storage in oceans etc. which help rebalancing, or taking over a process – but in some sense it is clear that rapidly changing amounts of respective cycle components (like less plants or more humans etc.) might lead to a breakdown of all these natural balances/cycles and then lead e.g. to an accumulation of CO2.
Climatic changes due to planetary changes like changes in sun light or changes in magnetic field conditions or tectonic changes can disturb the above cycles but of course “geoengineering” like burning fossil fuels, employing fertilizers or some other large scale “disrupting innovation” or having rapid population growth may also disturb those cycles and it probably disturbs them faster and stronger than the current planetary changes. In some sense the discussion whether its bad that one effect is stronger than another is somewhat irrelevant, even if some people like to fight about this question. The relevant question is whether the combination is killing us sooner or later and to what degree.
January 3rd, 2020 at 9:35 am
There is a study which proves that N2O is harmless:
Biological effects of inhaled nitrogen dioxide in healthy human subjects
June 25th, 2020 at 6:01 pm
nad wrote
It is important to align terminologies. Please observe that the term “Geoengineering” comprises: “Methods that aim to deliberately alter the climate system to counter climate change” (see p. 29). In particular “Burning fossil fuels” is the opposite of geoengineering. Burning fossil fuels led to climate change and has thus made the deployment of counter actions necessary and these may be in the form of geoengineering.
If you want to go on and boost your literacy on the subject of geochemical cycles I recommend the publications of the Environmentall Literacy Council. In particular I cite from the page “Biogeochemical Cycles”:
….and as you already similarily said:
So we need to understand those disturbances of “cycling” better and thus as a start one should make sure that one is talking about the same things.
August 9th, 2020 at 10:19 am
Na, wie schlimm ist das wohl?!
September 3rd, 2020 at 9:42 am
Tracy Pearson wrote:
Well I guess this is quite a simplification. I don’t know, but eventually it was stated as such in order to make major cycle mechanisms better accessible to a broad audience. That is I guess the phenomen of hydrogen escape seems small but certainly it seems -especially in the long run- not negligable.