symmetries II – Fano plane
assume the world was a simple one: Assume most of the numbers you know where not there (and the numbers you don’t want to know as well) only 0 and 1 where left. To have this work out reasonable we will have to accept such things as 1+1 = 0., but besides the fact that all people would have to share two mobile numbers one can still do geometry in such a world: In the three dimensional space each point can be localized by three numbers (called a triple and usually denoted by (x,y,z)). Now we only have two numbers for each of the three giving us a total of 3^2 = 8 possible points in that world. Now let us have a look at all the straight lines through (0,0,0) in this world of 8 points. You will find seven of them and each one will have only two points in it (the bare minimum for a straight line).
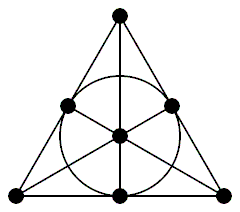
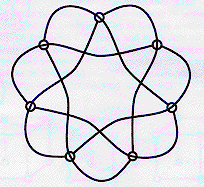
The set of straight lines (you can call them one dimensional subspaces if you like) forms itself an abstract plane (a projective plane to be precise) and in the case of our simple 0-1-world this plane is called the Fano plane. The above images both show a model of that abstract plane: It has seven points and seven lines (the points given by our seven one-dimensional subspaces of our world, and the lines defined by the twodimensional subspaces, which are seven). Each line runs through 3 points and each point is on three lines. However one should not take the “straight” too seriously here it is there merely for the lack of a better name. Instead one should think of these straight lines simply as subsets of the set of points, each having three points in it, and any two of these straight-lines will have exactly one point in common.
Now todays question is: How many symmetries does this Fano plane have?
A symmetry is a mapping which “doesnt change” things. Like e.g. the letter “A” looks the same also if seen in a mirror.
Here a symmetry is exchanging the points in such a way that lines are mapped into lines, that is if three points formed a line, after the permutation the three shall still form a line.
While the left image shows the Fano plane in a way one might come up with when trying to meet the above requirements, and where almost all lines are drawn straight (except one which is shown as a circle due to the lack of extra directions) the right reveals the sevenfold symmetry showing that indeed there is no special point in the plane.
Both images reveal some of the symmetries (in the left one can for example mirror the figure along the lines through the center point, and on the right we have some rotational symmetry as well as mirror symmetries) but they will not reveal the total of 168 different possibilities.
There is a nice page at John Baez’s blog about Klein’s quartic curve and the Fano plane with its symmetries (the above images are from there)
this is a followup to symmetries I – mirror symmetry.